Draw 1 8th of a Circle in C
A cardinal operation in computer graphics is to draw lines and circles. For case, these are used equally the components of scalable fonts and vector graphics; the letter "g" is specified as a series of lines and curves, so that when you zoom in on it the computer can redraw it at whatever resolution is needed. If the system simply stored the pixels for the letter of the alphabet shape, then zooming in would consequence in a low quality paradigm.
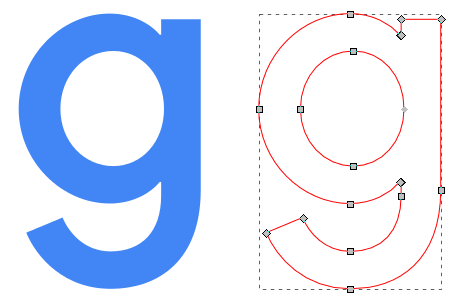
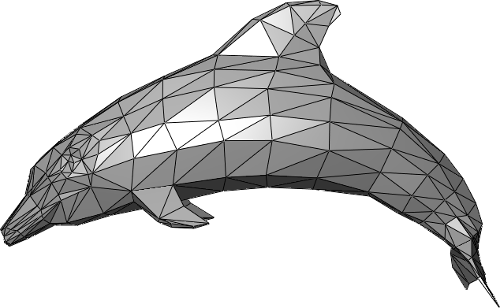
In 3D graphics shapes are oftentimes stored using lines and curves that mark out the edges of tiny flat surfaces (commonly triangles), each of which is so minor that you can't run across them unless you zoom correct in.
The lines and circles that specify an object are usually given using numbers (for example, a line betwixt a given starting and finishing position or a circle with a given centre and radius). From this a graphics program must calculate which pixels on the screen should be coloured in to represent the line or circle, or it may just need to work out where the line is without drawing information technology.
For case, here's a filigree of pixels with five lines shown magnified. The vertical line would have been specified as going from pixel (2, nine) to (2, 16) – that is, starting 2 across and 9 up, and finishing 2 across and sixteen upwards. Of form, this is only a small role of a screen, every bit normally they are more than like 1000 by thou pixels or more than; even a smartphone screen is hundreds of pixels high and wide.
These are things that are easy to do with pencil and paper using a ruler and compass, only on a computer the calculations demand to be done for every pixel, and if you use the wrong method and then it will have too long and the image will be displayed slowly or a alive animation will appear jerky. In this section we will wait into some very unproblematic but clever algorithms that enable a reckoner to do these calculations very quickly.
To describe a line, a computer must work out which pixels need to exist filled and so that the line looks straight. Y'all tin try this past colouring in squares on a grid, such as the one below (they are many times bigger than the pixels on a normal printer or screen). We'll identify the pixels on the grid using two values, (x, y), where x is the distance across from the left, and y is the altitude up from the bottom. The bottom left pixel beneath is (0, 0), and the top right 1 is (xix, 19).
Endeavour to draw these direct lines past clicking on pixels in the following grid:
- from (2, 17) to (10, 17)
- from (18, ii) to (18, 14)
- from (1, 5) to (8, 12)
Drawing a horizontal, vertical or 45 degree line like the ones in a higher place is easy; it'southward the ones at different angles that require some calculation.
Without using a ruler, can y'all draw a direct line from A to B on the post-obit grid by colouring in pixels?
Once you have finished cartoon your line, endeavour checking it with a ruler. Identify the ruler then that it goes from the heart of A to the heart of B. Does information technology cross all of the pixels that you take coloured?
The mathematical formula for a line is . This gives you the y value for each ten value across the screen, and you get to specify ii things: the gradient of the line, which is , and where the line crosses the y axis, which is . In other words, when you are x pixels beyond the screen with your line, the pixel to colour in would exist (, ).
For instance, choosing and means that the line would go through the points (0, three), (1, five), (two, vii), (3, 9) and then on. This line goes up 2 pixels for every one across , and crosses the y axis 3 pixels up ().
Yous should experiment with drawing graphs for various values of and (for instance, start with , and try these three lines: , and ) by putting in the values. What angle are these lines at?
The formula tin be used to work out which pixels should exist coloured in for a line that goes between and . What are and for the points A and B on the filigree below?
Come across if y'all tin can piece of work out the and values for a line from A to B, or you can calculate them using the following formulas:
Now draw the same line as in the previous section (between A and B) using the formula to calculate for each value of from to (you volition demand to round to the nearest integer to work out which pixel to colour in). If the formulas accept been applied correctly, the value should range from to .
Once you take completed the line, check it with a ruler. How does it compare to your first endeavour?
At present consider the number of calculations that are needed to work out each point. It won't seem like many, only remember that a computer might exist computing hundreds of points on thousands of lines in a complicated epitome. Although this formula works fine, it's too slow to generate the complex graphics needed for good animations and games. In the next section we will explore a method that greatly speeds this up.
A faster mode for a computer to calculate which pixels to colour in is to use Bresenham'south line algorithm. Information technology follows these simple rules. First, calculate these three values:
To draw the line, fill the starting pixel, and then for every position along the x axis:
- If is less than 0, draw the new pixel on the same line as the concluding pixel, and add together to .
- If was 0 or greater, draw the new pixel ane line higher than the last pixel, and add together to .
- Echo this determination until nosotros reach the terminate of the line.
Without using a ruler, utilize Bresenham's line algorithm to draw a straight line from A to B:
In one case you have completed the line, check information technology with a ruler. How does it compare to the previous attempts?
Then far the version of Bresenham's line drawing algorithm that you have used only works for lines that have a gradient (slope) between 0 and 1 (that is, from horizontal to 45 degrees). To make this algorithm more than general, then that information technology tin can be used to depict whatever line, some additional rules are needed:
- If a line is sloping downwardly instead of sloping upward, so when P is 0 or greater, depict the side by side column'due south pixel ane row below the previous pixel, instead of above it.
- If the alter in value is greater than the alter in value (which means that the slope is more than ane), then the calculations for A, B, and the initial value for P will demand to be changed. When computing A, B, and the initial P, utilise X where you previously would have used Y, and vice versa. When drawing pixels, instead of going beyond every column in the X axis, get through every row in the Y centrality, drawing one pixel per row.
In the filigree in a higher place, cull two points of your own that are unique to you. Don't only choose points that will give horizontal or vertical lines!
Now use Bresenham's algorithm to draw the line. Bank check that it gives the same points as you would have chosen using a ruler, or using the formula . How many arithmetic calculations (multiplications and additions) were needed for Bresenham'south algorithm? How many would have been needed if you lot used the formula? Which is faster (deport in listen that adding is a lot faster than multiplying for most computers).
Yous could write a program or design a spreadsheet to do these calculations for yous – that'south what graphics programmers accept to do.
Also as straight lines, another common shape that computers often need to draw are circles. An algorithm similar to Bresenham'due south line drawing algorithm, called the Midpoint Circumvolve Algorithm, has been adult for drawing a circumvolve efficiently.
A circumvolve is defined by a middle bespeak, and a radius. Points on a circle are all the radius altitude from the centre of the circle.
Try to draw a circle by hand by filling in pixels (without using a ruler or compass). Notation how hard it is to brand the circle await circular.
It is possible to draw the circumvolve using a formula based on Pythagoras' theorem, but it requires computing a foursquare root for each pixel, which is very slow. The following algorithm is much faster, and but involves unproblematic arithmetic so information technology runs quickly on a calculator.
Here are the rules for the midpoint circle algorithm for a circle around (, ) with a radius of :
Repeat the following rules in order until becomes greater than :
- Fill the pixel at coordinate (, )
- Increase by
- Increment by one
- If is greater than or equal to 0, subtract from , and and then decrease one from .
Follow the rules to draw a circumvolve on the grid, using (, ) as the centre of the circle, and the radius. Notice that it volition but draw the start of the circle so it stops because is greater than !
When becomes greater than , one eighth (an octant) of the circle is drawn. The balance of the circle tin be fatigued past reflecting the octant that you already have (yous tin can think of this equally repeating the pattern of steps you simply did in contrary). You lot should reverberate pixels along the X and Y centrality, so that the line of reflection crosses the centre of the centre pixel of the circumvolve. One-half of the circle is now drawn, the left and the right half. To add together the residuum of the circle, another line of reflection must exist used. Tin you piece of work out which line of reflection is needed to complete the circle?
Quadrants and octants Jargon Buster
A quadrant is a quarter of an surface area; the four quadrants that cover the whole area are marked off past a vertical and horizontal line that cantankerous. An octant is one eighth of an area, and the 8 octants are marked off by 4 lines that intersect at i point (vertical, horizontal, and two diagonal lines).
To complete the circle, you demand to reverberate forth the diagonal. The line of reflection should have a gradient of 1 or -1, and should cantankerous through the centre of the heart pixel of the circle.
While using a line of reflection on the octant is easier for a human to understand, a calculator can draw all of the reflected points at the aforementioned time it draws a point in the first octant considering when information technology is drawing pixel with an offset of (ten,y) from the centre of the circle, information technology can as well draw the pixels with offsets (ten, -y), (-x, y), (-10, -y), (y, x), (y, -x), (-y, x) and (-y, -10), which give all eight reflections of the original betoken!
By the way, this kind of algorithm can be adapted to draw ellipses, but information technology has to depict a whole quadrant considering yous don't take octant symmetry in an ellipse.
Computers need to draw lines, circles and ellipses for a wide variety of tasks, from game graphics to lines in an architect's drawing, and even a tiny circle for the dot on the top of the letter 'i' in a word processor. Past combining line and circle drawing with techniques like 'filling' and 'antialiasing', computers tin describe smooth, clear images that are resolution independent. When an image on a figurer is described as an outline with make full colours it is called vector graphics – these can be re-drawn at whatever resolution. This means that with a vector image, zooming in to the image will not cause the pixelation seen when zooming in to bitmap graphics, which only store the pixels and therefore make the pixels larger when you zoom in. Nonetheless, with vector graphics the pixels are recalculated every fourth dimension the paradigm is redrawn, and that'southward why it's important to use a fast algorithm like the ane higher up to draw the images.
Outline fonts are ane of the most mutual uses for vector graphics as they allow the text size to exist increased to very large sizes, with no loss of quality to the alphabetic character shapes.
Computer scientists take found fast algorithms for drawing other shapes too, which ways that the prototype appears apace, and graphics tin can display quickly on relatively wearisome hardware – for example, a smartphone needs to practice these calculations all the time to brandish images, and reducing the amount of calculations tin can extend its bombardment life, as well as make information technology appear faster.
As usual, things aren't quite as elementary equally shown hither. For example, consider a horizontal line that goes from (0, 0) to (10, 0), which has eleven pixels. Now compare it with a 45 degree line that goes from (0, 0) to (10, 10). It yet has 11 pixels, simply the line is longer (about 41% longer to be precise). This means that the line would appear thinner or fainter on a screen, and extra work needs to be done (mainly anti-aliasing) to make the line look ok. Nosotros've but only begun to explore how techniques in graphics are needed to quickly render high quality images.
Line and circle cartoon Project
To compare Bresenham's method with using the equation of a line (), choose your own start and end betoken of a line (of course, make sure it's at an interesting angle), and bear witness the calculations that would be fabricated by each method. Count upwardly the number of additions, subtractions, multiplications and divisions that are made in each example to make the comparison. Annotation that addition and subtraction is usually a lot faster than multiplication and division on a estimator.
You can judge how long each operation takes on your calculator by running a program that does thousands of each operation, and timing how long information technology takes for each. From this you tin estimate the full fourth dimension taken by each of the two methods. A good measurement for these is how many lines (of your chosen length) your computer could summate per second.
If yous're evaluating how fast circle drawing is, you can compare the number of add-on and multiplication operations with those required by the Pythagoras formula that is a basis for the simple equation of a circle (for this adding, the line from the centre of the circle to a particular pixel on the edge is the hypotenuse of a triangle, and the other two sides are a horizontal line from the middle, and a vertical line upwardly to the indicate that we're wanting to locate. You'll need to summate the y value for each x value; the length of the hypotenuse is always equal to the radius).
Source: https://www.csfieldguide.org.nz/en/chapters/computer-graphics/drawing-lines-and-circles/
0 Response to "Draw 1 8th of a Circle in C"
Post a Comment